Моделируем удержание пользователей: в поисках оптимальной формулы

Каким бы ни был ваш продукт (онлайновым или оффлайновым, для веба или мобильным, игрой или сервисом), показатели удержания пользователей в нём будут играть важнейшую роль.

Удержание – это метрика качества продукта, которая отражает лояльность пользователей к вам, их желание остаться с вами спустя некоторое время.

Под показателем удержания мы понимаем классический «retention» N-го дня – долю пользователей, которые пользуются продуктом и спустя N дней после своего первого визита.

Допустим, 1 апреля вашу игру впервые запустило 100 пользователей. Из них кто-то даже не запускал туториал, кто-то начал обучение и не закончил его, а кто-то прошел его полностью.

И 2 апреля из этих 100 пользователей к вам вернулось, допустим, 40. Таким образом, мы говорим, что удержание первого дня равен 40% (кстати, вполне неплохо, у успешных игр как раз значение в 40% и является ориентиром).

А 8 апреля из этих 100 пользователей к вам пришло лишь 15. Это значит, что удержание седьмого дня = 15%.

График показателя удержания пользователей имеет схожий вид и для веб-приложений, и для мобильных приложений, и для интернет-магазинов, и для многих оффлайн-продуктов:

• в первые дни (недели, месяцы) он резко падает: пользователи не успевают пройти «onboarding» (здесь – адаптация, – прим.редакции) и не остаются в проекте;
• затем те, кто всё же остался, понемногу отпадают, но уже не с такой скоростью, как в самом начале;
• наконец, когда база пользователей уже сформирована, график выходит в плато, которое лишь едва снижается, и чем больше прошло времени, тем больше график похож на горизонтальную линию.

Графически график удержания выглядит примерно так:

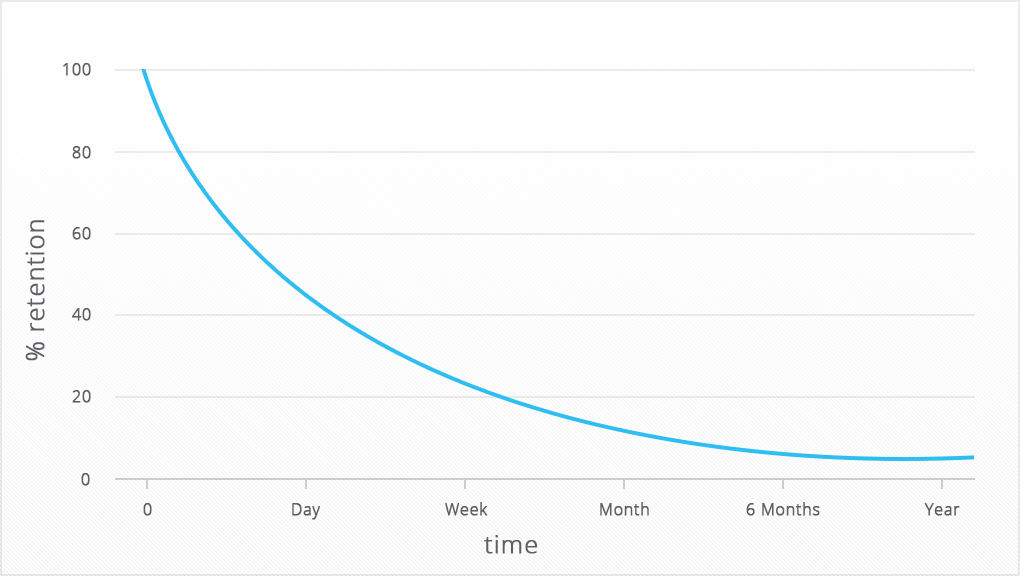
Такую кривую ещё называют «forgetting curve», потому что ею же описывается процесс забывания человеком полученной информации.

Иногда может возникнуть следующая ситуация: у вас есть значения удержания за какие-то фиксированные периоды (1 день, 7 дней, 30 дней), и вы хотите узнать значения показателя за промежуточные периоды (6 дней, 14 дней, 23 дня) или после них (35 дней). Это может пригодиться, если вы хотите прогнозировать «lifetime» или LTV (Lifetime Value), а также просто рассчитать, сколько пользователей из ныне активных будут активны в будущем.

Как же быть, если стоят такие задачи?

В статье мы как раз хотим поделиться своим опытом решения этой проблемы.

В этом случае вам предстоит смоделировать эту гиперболу самостоятельно и по модельному значению отвечать на интересующие вас вопросы.

Помните, в школе вы строили кривые по точкам? Вот именно здесь эти знания вам и пригодятся. Единственное что – будьте готовы к тому, что в итоге уравнения будут чуть сложнее, чем в школе.

Для начала подготовим программы, которыми будет для этого использовать. Мы, к слову, специально выбрали бесплатные и общедоступные инструменты для решения задачи, чтобы вы впоследствии могли сделать то же самое самостоятельно «без СМС и регистрации»:

• Open Office, а именно его электронные таблицы и «Решатель» (Solver) во вкладке «Сервис»;
• «Нелинейный решатель», который нужно поставить отдельным бесплатным плагином.

Еще мы будем пользоваться механизмом аппроксимации, то есть приближением фактических значений математическими формулами. Делая аппроксимацию, важно, во-первых, выбрать правильную функцию (которая бы изгибалась в нужных местах) и, во-вторых, верно подобрать её коэффициенты, чтобы разница между моделью и фактом была минимальной.

Итак, какой же из функций можно аппроксимировать удержание?

На ум (тем, кто заканчивал школьный курс математики) приходит гипербола, и это верная ассоциация.

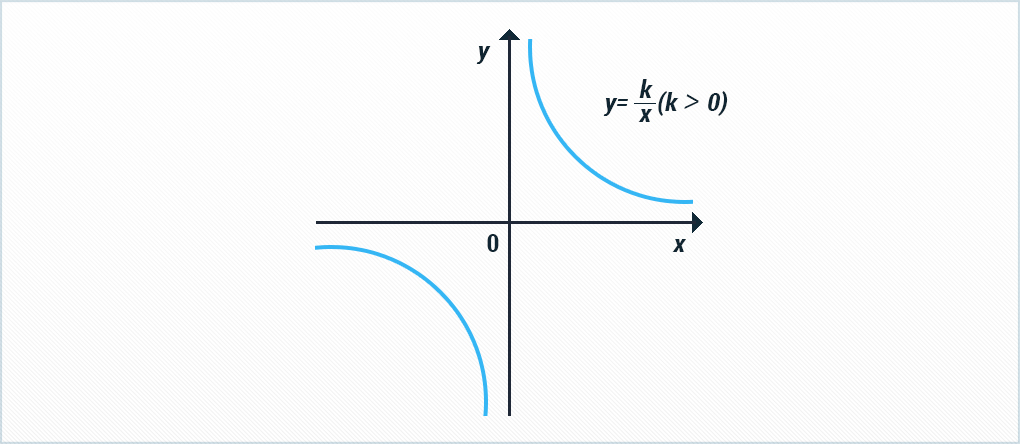
Рассмотрим несколько гиперболических уравнений (X в уравнении означает номер периода: дня, недели, или месяца). Начнём с простого уравнения гиперболы A/X, затем будем усложнять его, добавляя различные коэффициенты:

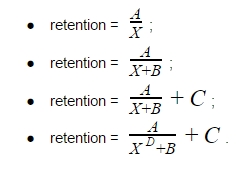
Неизвестные A, B, C, D – это коэффициенты, которые нам предстоит найти.

Но наша задача состоит не только в этом. Найдя в каждой из формул значения коэффициентов, мы затем должны будем выбрать самое оптимальное из этих уравнений.

То есть, итог каждого из уравнений – отдельная кривая. Мы будем сравнивать эту кривую с фактическими значениями (которые, надо сказать, не всегда идеально вписываются в модель) и выбирать ту из кривых, которая лучше повторяет факт.

Критерием будет минимум суммы квадратов отклонений (что означает, что мы воспользовались методом наименьших квадратов) между фактическими и модельными значениями (метод наименьших квадратов уже выходит за школьную программу, речь про раздел теории оценивания в математической статистике – это преподают уже в высших учебных заведениях, – прим. редакции).

В Excel это делается с помощью СУММКВРАЗН (SUMXMY2), а в Open Office эта функция нами не обнаружена, но это не проблема: рассчитываем в отдельном столбце отклонения (просто как разность между модельными и фактическими значениями), возводим их в квадрат, затем суммируем квадраты отклонений.

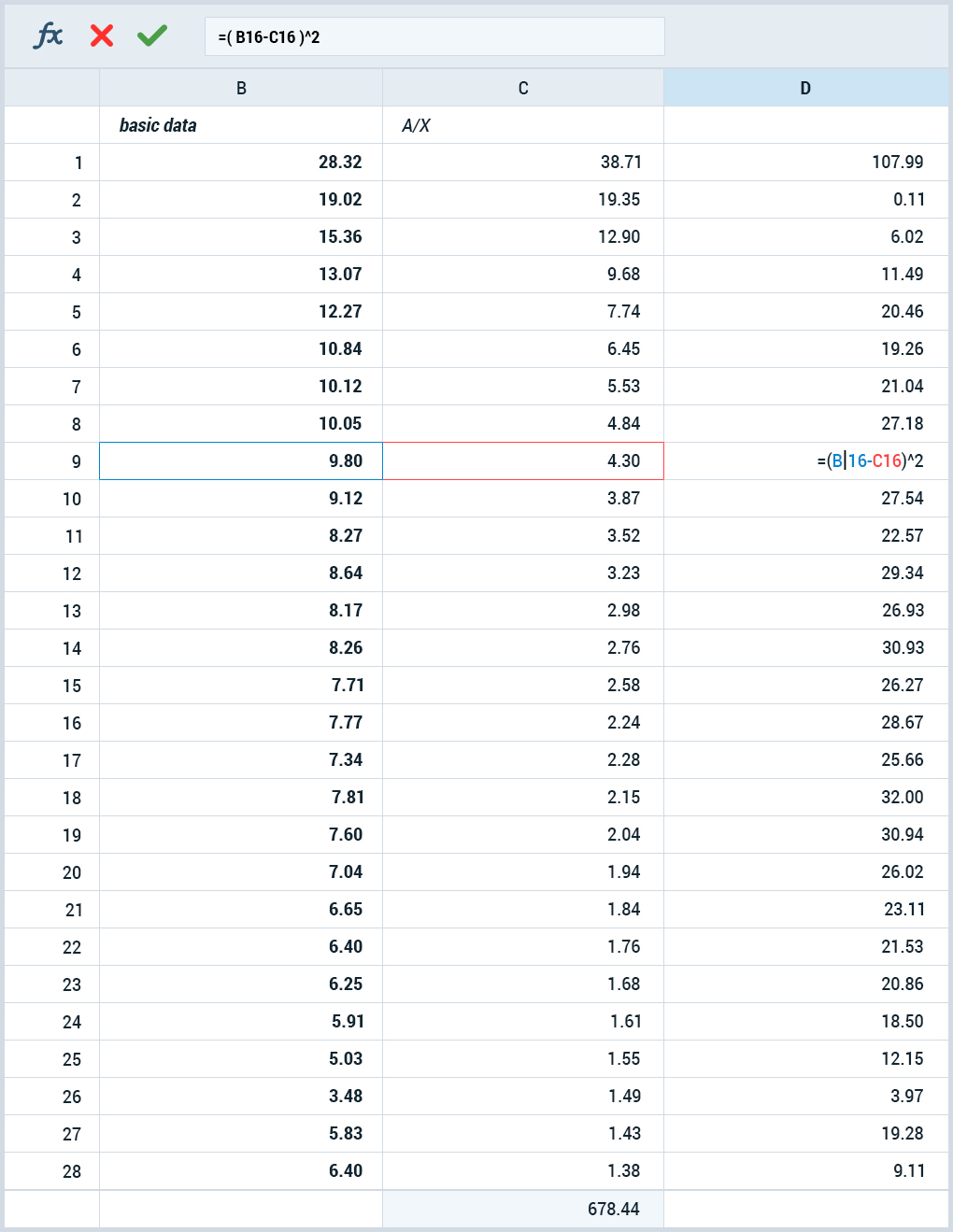
Для оптимизации нам пригодится Solver. Притом, учитывая и квадраты отклонений, и гиперболический вид функции, нужен именно нелинейный.

Здесь и далее мы пользовались поочерёдно DEPS Evolutionary Algorithm и SCO Evolutionary Algorithm, за стартовые данные новой итерации брали значения коэффициентов, полученные на предыдущей итерации. Процесс заканчивался тогда, когда сумма квадратов отклонений с новой итерацией уменьшалась не более чем на 0,01.

За исходные данные возьмём удержание демо-проекта devtodev (вы можете повторить всё то же самое самостоятельно, демо доступно без регистрации) за 28 дней.

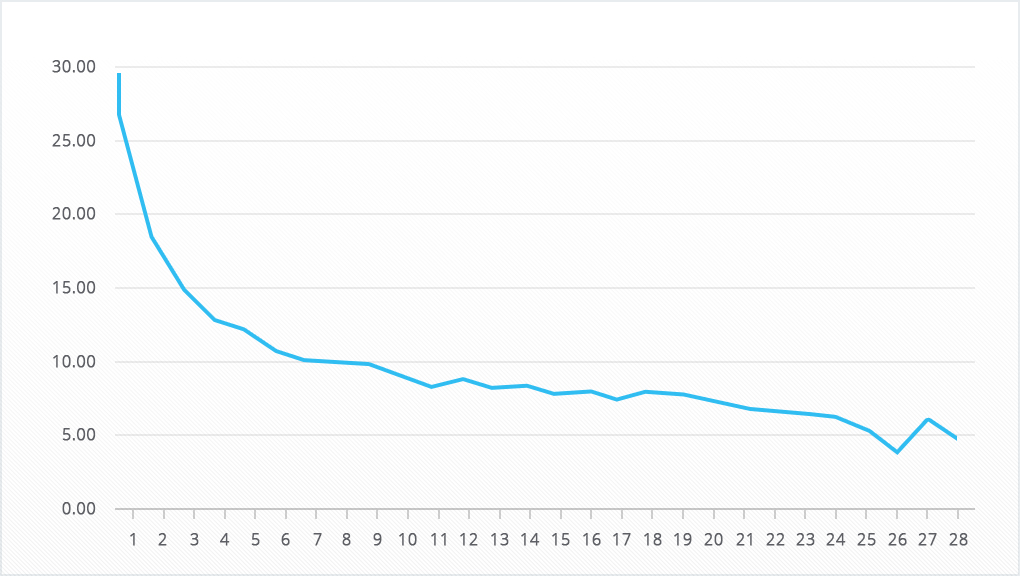
Как видно из графика, данные далеко не идеальны, и для нашей задачи это отлично подходит. Редко на практике вы получаете в руки идеальные данные, а задачу решать всё равно надо.

Будем пытаться для каждой из выбранных функций подобрать такие значения коэффициентов, чтобы построить кривую, как можно более близкую к исходным данным.

Вот что получается:

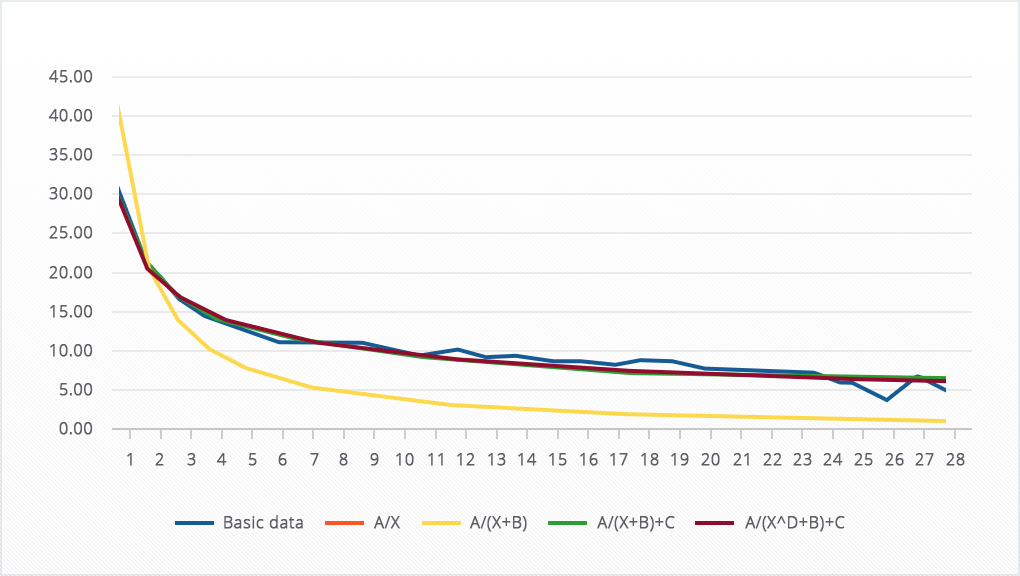
Как видно, жёлтая (A/(X+B)) и красная (A/X) линии совпали, но от исходной кривой они очень далеки, а вот зелёная (A/(X+B)+C) и бордовая ((A/(X↑D+B)+C) линии довольно точно повторили исходную кривую. При этом бордовая линия, если судить по сумме квадратов отклонений, повторяет стартовые данные точнее всего:

Таким образом, мы прощаемся с уравнениями A/(X+B) и A/X и идём дальше.

Если обратить внимание на кривую, то видно, что с каждым днём она меняется всё меньше. Нам это напомнило про логарифмическую кривую, и мы подумали: а что если вместо X в уравнение подставить LN(X), не улучшит ли это наши результаты?

Поэтому следующим шагом давайте сравним результаты лучшей функции с X и LN(X). Единственное, что в одном из случаев добавим под логарифм коэффициент E:

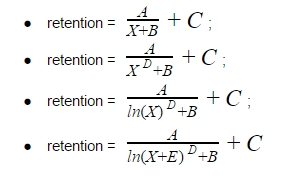
Визуально все четыре кривые справились достаточно неплохо, однако давайте всё же рассмотрим квадраты отклонений:

Какие выводы можно сделать?

• лучше всего аппроксимируют кривые с четырьмя и пятью переменными;
• замена X на LN(X) пусть и немного, но улучшает аппроксимацию.

На этом этапе мы прощаемся с кривой A/(X+B)+C. Она не выдержала конкуренции.

Остались три кривые, однако неизвестно, как они работают на длинных дистанциях. Мы тестировали их лишь на первых 28 днях. Вполне вероятен случай, что если вместо X подставить большое значение (скажем, 365), то они уйдут в минус, что невозможно по определению удержания.

Поэтому, раз уж мы определили трёх финалистов, давайте следующим этапом протестируем, как они могут справляться с более долгосрочным удержанием. Мы просто взяли несколько примеров долгосрочного удержания из интернета и протестировали наши кривые на каждом из них:

• за 12 недель;
• за 18 месяцев (осторожно, LinkedIn, для просмотра надо будет поставить VPN-расширение на браузер, – прим. редакции);
• за 720 дней.

Пример про 720 дней рассмотрим графически.

Данные были взяты из статьи “How to measure the success of your app”, и в данном случае мы пытались повторить приведённую статистику по удержанию в социальной сети:

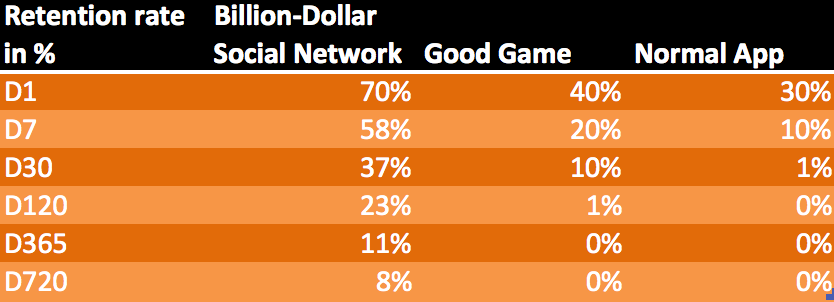
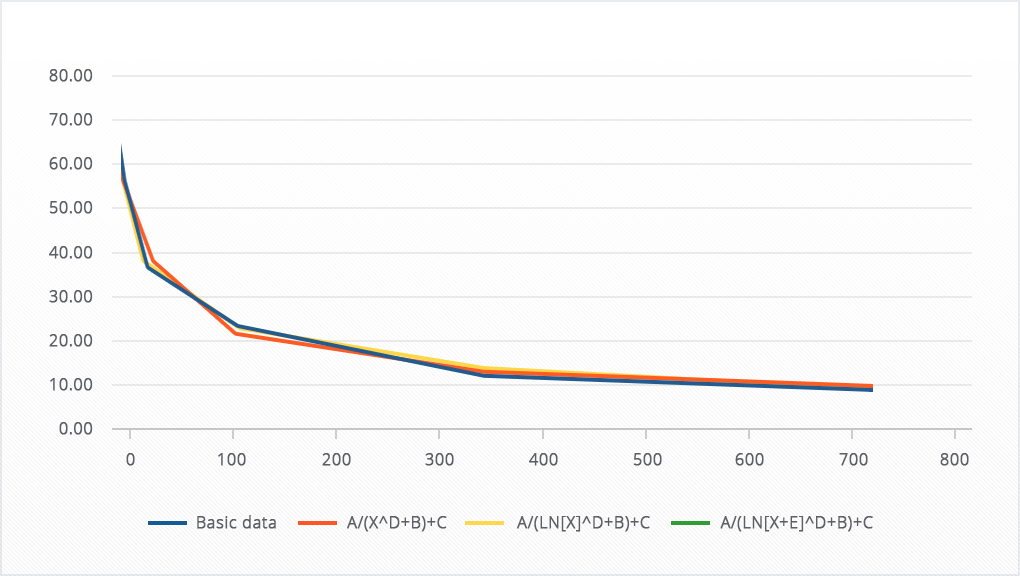
Видно, что все три кривые хорошо справились с аппроксимацией, однако красная линия немного сильнее выдаётся на фоне синей — отклонение у неё максимальное.

Теперь делимся результатами по всем трём примерам (напомним, чем меньше сумма квадратов отклонений, тем лучше):

Если бы это был чемпионат, то победила бы последняя кривая. Однако, согласитесь, её преимущество не так явно, особенно учитывая, как ненамного отличаются друг от друга значения суммы квадратов отклонений. Поэтому победителями (как на детском празднике) мы признаем все три кривые, и все три кривые мы можем рекомендовать для аппроксимации удержания.

Также хотелось бы рассказать про значение каждого из коэффициентов на примере функции A/(ln(X)↑D+B)+C.

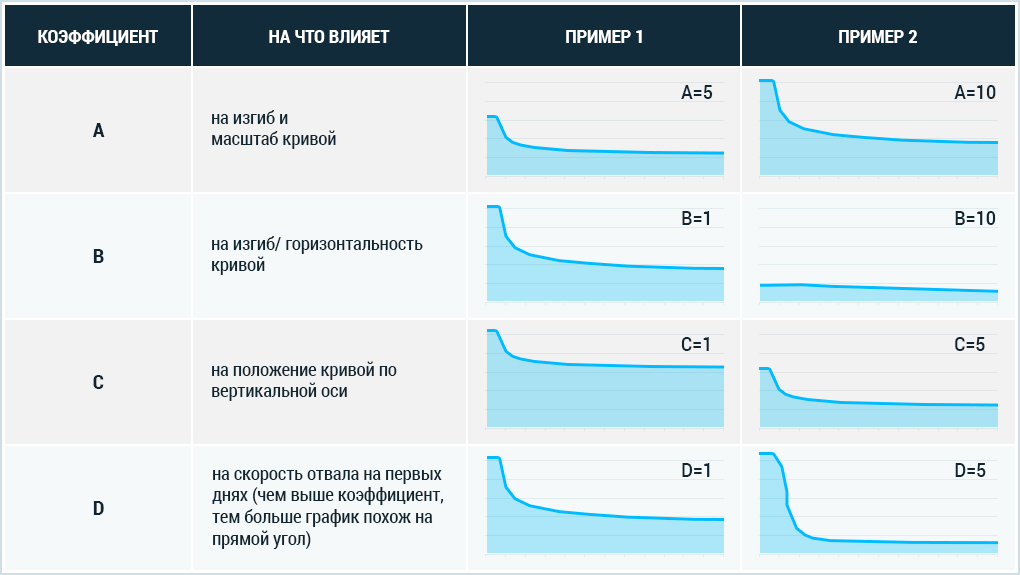
Вывод, к которому мы приходим, следующий: для аппроксимации retention хорошо подходят три вида кривых:

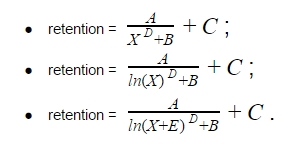
Победителей мы огласили, теперь хотим огласить несколько важных моментов, которые нужно иметь в виду при аппроксимации удержания.

1). Если у вас мало исходных точек, то лучше использовать ту кривую, в которой меньше коэффициентов. И запомните: никогда не используйте кривую, у которой неизвестных коэффициентов больше, чем у вас точек! Скажем, если у вас есть лишь три точки удержания (допустим, день 1, день 7, день 28), то максимальное количество коэффицентов, которые вы можете использовать – это три, и в этом случае лучше всего подойдет функция A/(X+B)+C.

2). Вы всегда вольны менять оптимизационную функцию так, как вам вздумается (мы воспользовались стандартным МНК и использовали простую сумму квадратов отклонений). Допустим, вам не так важно поведение удержания в другие периоды, но вы хотите, чтобы модельное и фактические значения удержания точь-в-точь совпали на 180 днях. Поэтому для оптимизационной функции отклонение на 180 днях можно взять с большим коэффициентом или в большой степени.

3). Мы даём вам не универсальную рекомендацию, а просто наш опыт решения нескольких разовых задач. Не исключено, что есть и другие функции, более точно аппроксимирующие показатели удержания. Но те функции, которые использовали мы, дали хороший результат.

Файл со всеми расчётами вы можете скачать по ссылке.

В завершение статьи хотим пожелать, чтобы уровень удержания в вашем проекте всегда оставался непредсказуемо высоким.