Виральность как вирус

Лучшая математическая модель вирусного маркетинга

Современные модели вирусного маркетинга для бизнес-сообществ базируются на ошибочных предположениях. В результате, сами модели не могут отразить реального положения дел.

Но как бизнес-сообщество может построить реалистичную модель вирусного маркетинга? Как узнать, какие факторы (вирусный коэффициент, временной масштаб, отток пользователей, размер рынка) наиболее важны? К счастью, у нас есть много литературы о математических моделях вирусного роста (и спада), труды, которые издавались с 1927 года. Эти модели идеально подходят, когда разговор заходит об изменениях в размере рынка и вероятности возврата бывшего пользователя. Очевидно, что в то время никто не думал о видео на YouTube или приложениях для iPhone в том время, когда у телефонов были еще провода и диски для набора номера. Эти модели описывают распространение… вирусов.

Модель

Классическая SIR модель распространения заболевания сделана Кермаком и МакКендриком (Kermack и McKendrick). Я применила ее к вирусному маркетингу, проведя аналогию между заболеванием и продуктом. Получающийся на выходе результат, конечно, сильно отличается, но математика одна.

Кермак и МакКендрик разделили общую популяцию на рынке, N, на три группы.

• S – количество людей, восприимчивых к болезни (потенциальных клиентов);
• I – количество пораженных заболеванием (текущие клиенты);
• R – количество выздоровевших (бывшие клиенты).

Количество людей в этих популяциях изменяется со временем. Потенциальные клиенты становятся текущими в результате успешных приглашений. Текущие становятся бывшими, если они прекращают использование продукта. Для упрощения, я приняла общий объем рынка, N=S+I+R, как число постоянное, а бывших клиентов как получивших иммунитет. Параметрами, которые регулируют распространение болезни, являются:

• β – скорость инфекции (уровень обмена);
• γ – скорость выздоровления (уровень оттока).

Предположим, что текущие потребители, I, и потенциальные, S, общаются друг с другом с таким уровнем, который пропорционален их числу (что регулируется Законом действующих масс). Таким образом, количество новых потребителей, приходящих к нам от сарафанного радио или шаринга в соц.сетях в единицу времени можно подсчитать как βSI. Количество наших пользователей увеличилось на βSI, а количество потенциальных уменьшилось на то же число. Это играет ту же роль, что и «Коэффициент виральности» в модели Скока, но объясняет и тот факт, что уровень конверсии от шаринга замедляется, когда доля людей, которые уже попробовали продукт, увеличивается. Кроме того, мы отказываемся от концепции «цикличности времени». Вместо этого мы используем среднее время, которое требуется на то, чтобы поделиться чем-то и средняя частота, с которой люди делают это, что учитывается единицей времени в знаменателе β. Таким образом, β представляет собой число успешных приглашений текущим пользователем потенциального клиента в единицу времени (например, час, день, неделя). Я думаю, что это более надежное определение коэффициента виральности, нежели то, что использовали Райс и Скок, так как моделирование вирусного обмена на основе среднего во времени обуславливает следующие факты:

• Пользователи не делятся синхронизированными партиями;
• Каждый пользователю нужно свое время для того, чтобы попробовать продукт, полюбить его и поделиться с друзьями. Вместо того, чтобы задать время цикла равным для всех, β представляет собой среднюю скорость обмена;
• Пользователи могут приглашать других при первой же попытке или же после того, как они долго его использовали.

В этой модели текущие пользователи становятся бывшими со скоростью, которая определяется параметром γ. Таким образом, γ это та часть текущих пользователей, которая стала бывшими за единицу времени. Она обратно пропорциональна времени (1/t), а 1/γ это среднее время, в которое пользователь остается пользователем. Так что если γ = 1% (пользователей теряется в сутки), то среднее время жизни пользователя составляет 100 дней.

Дифференциальные уравнения для распространения вируса:

• dS/dt=−βSI
• dI/dt=βSI–γI
• dR/dt=γI

Анализируя уравнения

Это нелинейные дифференциальные уравнения, которые невозможно удобно решить для получения формул S(t), I(t) и R(t) . Зато они могут показать динамику (особенно изменения размеров рынка и возвращающихся потребителей). Вы можете многое понять изучив их и проинтегрировав численно. Давайте предположим, что t=0 представляет собой запуск нового продукта. Изначально только разработчики представляют его потребителей и являются пользовательской базой, I(0). Начальное число бывших потребителей R(0) равно 0, а все остальные являются потенциальными клиентами, S(0).

Сперва стоит отметить, что растущая пользовательская база (dI/dt>0) будет при βS/γ>1.

То есть, вирусный рост будет идти до тех пор, пока адресуемый рынок S(0) и скорость обмена β существенно выше скорости оттока γ. Модель показывает, что с достаточно большим рынком, вы можете испытывать вирусный рост даже при небольшом β, до тех пор, пока отток также невелик.

Если в t=0 количество S очень близко к N, то βS/γ примерно равно βN/γ. Таким образом, если βN/γ>1, то пользовательская база будет расти, если βN/γ<1 – не будет. Это эпидемиологической литературе его иногда еще называют как «основное репродуктивное число». Важно то, что «коэффициент виральности», как его называл Эрик Райс, также зависит от размеров рынка и оттока пользователей, как и от скорости вирусного обмена. Это примерно среднее количество новых потребителей, которых каждый пользователь пригласил в продукт в течение всего времени, пока он оставался пользователем, вот почему 1/γ. Однако, в случае вирусного роста, βN/γ быстро перестает представлять то количество клиентов, которых каждый пользователь пригласил.

Еще вы можете увидеть из этих уравнений, что если вы игнорируете изменение размеров рынка (приближение, которое имеет смысл для короткоживущих вирусных продуктов, вроде роликов YouTube), пользовательская база всегда сходится к 0 в течение длинного промежутка времени, если только у вас скорость оттока не равна 0. После того, как количество текущих клиентов достигнет пика dI/dt=0 при I=N–γ/β, скорость изменения пользователей станет отрицательной и их количество в конечном счете упадет до нуля. Это согласуется с данными Mashable о периоде полураспада постов Twitter и YouTube. Опять же, обратите внимание, что ключевую роль, которую играет отток в определении пика клиентов.

Примеры

Мы можем получить большее понимание этих уравнений, численно проинтегрировав их. В примерах единица времени для задачи β и γ это день, хотя вы можете выбрать произвольную. Я определи β как βN чтобы больше соответствовать концепции Райса о вирусном коэффициенте – если в момент t=0 количество S(0) примерно равно N, то βN это то количество новых потребителей, к которым обращается каждый существующий пользователь в день.

Задав:

N = 1 миллион людей на рынке.

βN = 10 инвайтов от пользователей в стуки

γ=50% пользователей теряется в стуки

I(0)=10 начальных пользователей

и численно проинтегрировав уравнения, приведенные выше, мы получим картину того, как меняется количество пользователей в течение первых 30 дней:

Этот график похож на распространение популярных Твитов, когда трафик резко вырастает и затем спадает, так как людям тема надоедает.

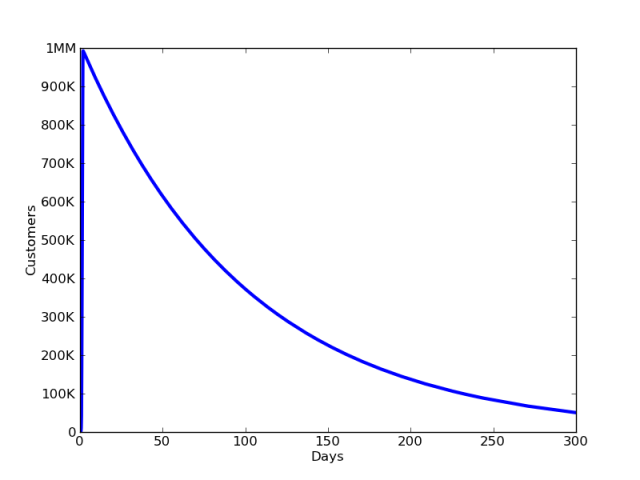
Для меньшего уровня оттока, γ=1% пользователей теряется в стуки, мы видим следующую картину на 300 дней:

Это показывает нам, что даже при малых значениях оттока, без новых потенциальных пользователей, приходящих на рынок, или без возвращения бывших, пользовательская база всегда уменьшается после достижения своего пика. Отметьте также, что меньший отток позволил нам добиться большего пика в трафике.

Как же можно поддержать устойчивый вирусный рост. Для этого вам надо понять, как вирусный маркетинг влияет на изменение размера рынка.

Статья вышла в рамках совместной серии материалов «Кодекс Freemium» сайтов по мобильной разработке App2Top.ru и Apptractor.ru. 

Оригинальный материал: http://datacommunitydc.org/blog/2013/01/better-science-of-viral-marketing-part-2/ 

Оригинальный перевод: http://apptractor.ru/marketing-monetization/engagement/luchshaya-matematicheskaya-model-virusnogo-marketinga.html