Одна из наиболее важных метрик любой условно-бесплатной игры — это Lifetime Value (LTV), совокупный доход игры, получаемый с одного клиента за все время. Как его вычислить, — в своей статье рассказал Исаак Роузбум (Isaac Roseboom), главный по анализу данных в deltaDNA. А наши друзья из SoftPressRelease перевели его труд на русский.

Вычисление точной ценности каждой установки – наиважнейший компонент бизнес-планирования F2P. Особенно если каждая установка может стоить вам $1-2. По этой причине многие издатели выделяют значительные ресурсы на разработку точных методов прогноза LTV. Как правило, эти методы попадают под один из трех подходов:
- Модель «ARPDAU»
- Модель «Транзакции»
- Модель «Игроки»
В первой модели прогнозируется доход по дням. Во второй – количество и величина транзакции на каждого игрока. И, наконец, в третьей модели используется историческая ценность игроков с одинаковыми демографическими показателями. Далее мы не только подробно поясним расчет каждой из этих моделей, но и подскажем вам, когда уместнее будет применить тот или иной подход.
1) Моделирование ARPDAU: простой подход
Наиболее распространенный подход – использование показателей <ARPDAU> и <Удержание> для определения LTV. Математически это выглядит так:
LTV = <ARPDAU> X <Итого дней в игре>
Среднее кол-во дней в расчете на установку рассчитывается из кривой удержания подбором степенной функции, т.е.:
R ∝ d — α
Существует несколько вариантов подбора α, однако, простейший из них – использование регрессии для подбора log (R) ∝ log (d). Не рекомендуется использование линейной регрессии, поскольку ошибки значений log (R) не имеют нормального распределения.
После определения степени наклона степенной функции, <Итого дней в игре> при d = D дней после установки, рассчитывается из интеграла от степенной функции удержания, т.е.:
<Итого дней в игре> =
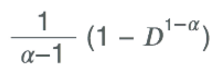
Это значение затем может быть использовано с ARPDAU для получения LTV.
В качестве учебного примера предположим, что ARPDAU = $0,1, а наше удержание от D1 до D7 равно 35%, 28%, 25%, 21%, 18%, 15% и 13%. Подбор по степенной функции дает α=1,3, что в свою очередь приводит к <Итого дней в игре> = 2,77 дней при D = 365 дней.
Это значит, что наша LTV = $0,28.
Данный метод расчета предполагаемой LTV, без сомнения, один из самых простых. Однако за эту простоту приходится мириться с некоторыми недостатками. Во-первых, в случае с долгоживущими играми ARPDAU будет основываться на уже существующих игроках, которые могут быть более склонны к покупкам, нежели группа, для которой вы пытаетесь выстроить прогноз. Вдобавок к этому, показатель удержания для всех игроков обычно хуже, чем для платящих игроков в частности. В конечном итоге это означает, что типичная погрешность при прогнозах с использованием данного метода составляет 30 — 40%, для групп от 500 игроков.
2) Моделирование транзакций: внимание на тех, кто платит
Более сложный подход предполагает моделирование количества транзакций, которые игрок осуществит за свою «жизнь».
Можно сконструировать статистическую модель, которая даст P (T|D), т.е. вероятность совершения игроком транзакции в день после установки D. Если Nt — количество транзакций, наблюдаемых в день = t, тогда в некий будущий день = D предполагаемое число транзакций составит:
Конверсия в плательщика может быть смоделирована аналогично, т.е. P (C|D) – вероятность того, что игрок станет плательщиком в день = D.
Эти вероятностные распределения могут быть описаны различными «длиннохвостовыми» распределениями. Для различных типов игр подходят различные распределения. Например, для ПК игр, как правило, хорошо подходят степенные функции, а для социальных казино-игр – гамма-распределение.
Эти модели могут быть составлены с использованием численных методов. Библиотеки в R и Python позволяют сделать это с легкостью. В R, функция fitdistr позволяет сопоставить набор вероятностных распределений с набором данных путем числового поиска параметров максимального правдоподобия. После получения наилучшего для моделей распределения, LTV в день = D может быть вычислен как
Где <T> — средняя величина внутриигровой покупки, ND – предполагаемое число транзакций на день = D, а CD – предполагаемое число конверсий на день = D.
Преимущество данного подхода состоит в том, что он моделирует поведение игроков, генерирующих LTV, то есть плательщиков. Точное моделирование конверсии первостепенно для игр, которые конвертируют множество игроков на поздних стадиях, например, MMO. Моделирование транзакций важно для игр с высоким числом транзакций на плательщика, т.е., для казуальных головоломок или других игр без премиум-валюты.
Хотя этот метод предполагает большую точность, нежели первый, он все же основывается на работе с группами, поэтому требует адекватный объем игроков для достижения точности, т.е. не может дать вам хороший метод расчета LTV индивидуального пользователя.
Если не принимать во внимание это ограничение, при условии использования подходящих распределений и тестирования, данный тип модели, как правило, достигает около 20% точности (для групп от 500 игроков).
3) Моделирование игроков: прогноз индивидуального LTV
Идеальным вариантом была бы возможность сделать достоверную оценку LTV каждого индивидуального игрока. Это не только позволило бы принимать решения по приобретению и рентабельности, но и изменило бы то, как игры взаимодействуют с игроками, например, игроки с низким LTV получали бы больше рекламы, а игроки с высоким LTV — VIP предложения.
Для прогнозирования LTV на уровне игрока необходимо использование большего количества подробной информации об игроке, включая демографические и поведенческие данные. Пример типа метрик, которые могут использоваться: страна, тип устройства, частота игровых сессий, уровень успехов, кол-во внутриигровых друзей и т.д.
Используя наборы данных за различные промежутки времени, эти метрики можно использовать при построении модели регрессии для расчета LTV. В зависимости от лежащих в основе распределений метрик, может использоваться одиночная модель, или игроки могут быть сегментированы на различные группы с различными характеристиками, например, может потребоваться использование абсолютно разных регрессионных моделей для игроков на iOS и Android.
Составленные модели можно использовать для прогнозирования LTV индивидуальных игроков. LTV группы может быть найден путем взятия среднего от индивидуальных предполагаемых LTV.
Все эти функции могут быть выполнены с использованием статистических пакетов в R или Python. В R, kmeans или hclust могут использоваться для сегментирования данных, а glm – для регрессии.
Очевидным преимуществом данного подхода является получение индивидуального LTV. Для достоверности результата, однако, нужны обширные, релевантные данные за большой промежуток времени. Это означает, что данный метод нельзя использовать во время запуска новой игры или после значительных обновлений игры.
Составление точных моделей
Хотя все три LTV модели могут показывать хорошие результаты, ответ на вопрос о том, какую модель использовать, зависит от ситуации, в которой находится ваша игра. Если у вас малое количество игроков с относительно краткой “жизнью” (например, несколько недель),тогда вам лучше всего подойдет модель 1).
Если у вас значительное количество игроков, и вы ожидаете большой разброс по “жизни” и структурам расходов в зависимости от группы, то необходима модель 2).
Наконец, если у вас хорошо зарекомендовавшая себя игра со стабильной версией и лояльными игроками, модель 3) может предложить значительные преимущества.
В любом случае, важнейшим моментом является тестирование ваших моделей на данных за прошедшие периоды времени с целью проверки их точности и понимания их ограничений. Напоследок отметим, что ни при каких условиях невозможно составить правдоподобные LTV модели из слишком маленькой выборки (например,<100 игроков). В подобных случаях приближенный метод типа LTV = 4 x ARPDAU скорее даст вам лучшее понимание, нежели любой из статистических подходов.
Источник: deltaDNA
Перевод: SoftPressRelease

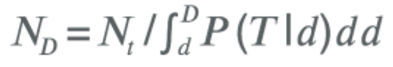

Комментарии
Ответить